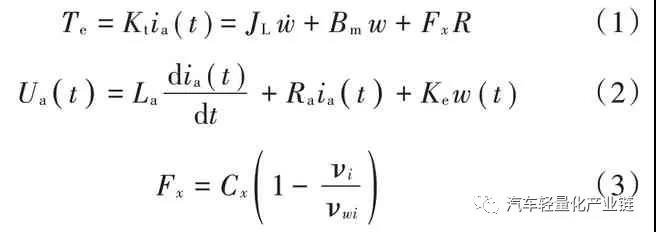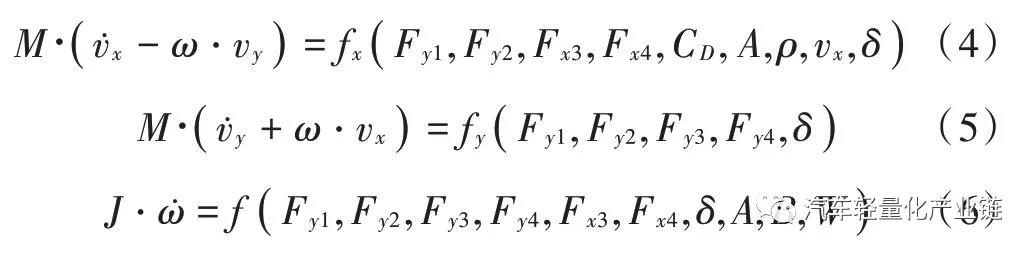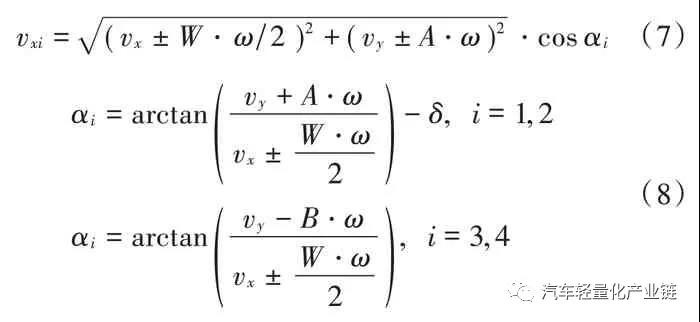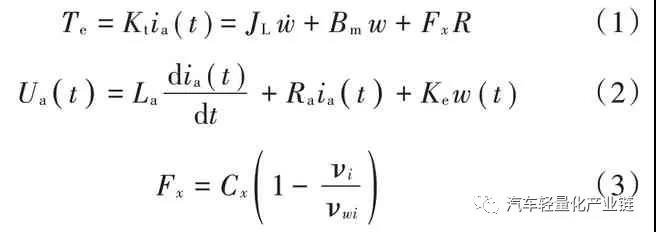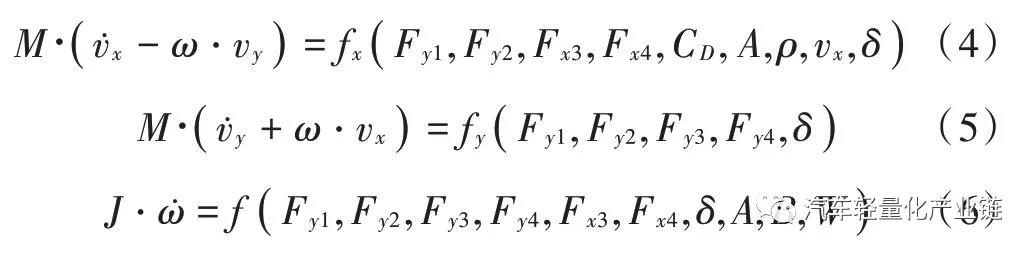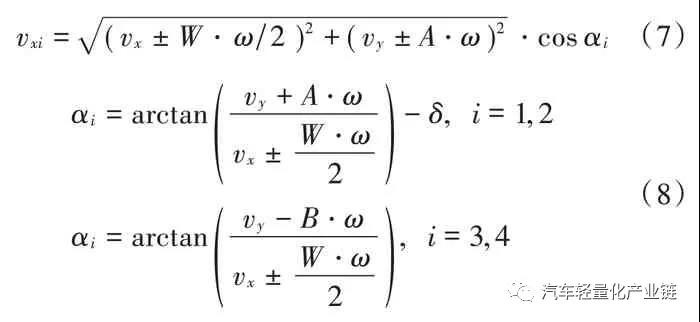鼓式制動器、摩托車剎車圈、Drum brake、輪轂剎車圈專業(yè)生產(chǎn)廠家無錫九環(huán)2022年1月25日訊 文中研究分布式后輪輪轂驅(qū)動電動汽車轉(zhuǎn)向控制特性。首先建立驅(qū)動電機和車輛動力學(xué)模型,分析簡化的動力學(xué)模型和非簡化動力學(xué)模型在不同轉(zhuǎn)角和速度時的輸入輸出特性。將整車動力學(xué)模型、兩個輪轂電機的機電特性模型集成起來,形成兩層三環(huán)節(jié)的控制。外層進行行駛速度反饋控制,內(nèi)層進行兩個電機轉(zhuǎn)速的反饋控制,外層的總行駛速度經(jīng)過速度分配,作為內(nèi)層兩個電機轉(zhuǎn)速的輸入分別控制兩個驅(qū)動電機,車輪的轉(zhuǎn)矩作為電機的負(fù)載轉(zhuǎn)矩輸入。最后對三種模型在兩種轉(zhuǎn)角變化工況下的動力學(xué)響應(yīng)進行對比分析。關(guān)鍵詞:輪轂電機;電動汽車;PID 控制;直流電機;電子差速;轉(zhuǎn)向控制輪轂電機是將電動機和制動系統(tǒng)集成在車輪上進行直接驅(qū)動的裝置,20 世紀(jì)60年代后期應(yīng)用于大型的礦用自卸車上。近幾年,隨著電動汽車的迅速發(fā)展,輪轂電機由于其控制靈活獨立、可以分別控制和協(xié)調(diào)各輪的運動,開始用于電動汽車形成分布式驅(qū)動的電動汽車。這種驅(qū)動形式的電動汽車在結(jié)構(gòu)上去掉了汽車底盤中的機械差速和隨動系統(tǒng)等傳動裝置,大大簡化了汽車的結(jié)構(gòu),降低了汽車的重量,是對傳統(tǒng)的集中驅(qū)動汽車結(jié)構(gòu)的較大革新,具有極大的應(yīng)用潛力,成為新型電動汽車的研究熱點。目前的研究主要有輪邊電機驅(qū)動與輪轂電機驅(qū)動兩種形式[1-2],輪轂電機驅(qū)動是將驅(qū)動電機直接安裝在車輪中,不占用車身空間,對電機和輪轂的設(shè)計和電機的控制要求都較高。為提高汽車的操縱性能和穩(wěn)定性,需要針對當(dāng)前的行駛狀態(tài)和駕駛員的駕駛指令,精確快速地控制每個輪的速度和扭矩,因此電機機電特性、硬件的響應(yīng)速度、轉(zhuǎn)向、加速、啟動、剎車時的速度或者扭矩的分配[3-4],都是要實時監(jiān)測或者協(xié)調(diào)控制的多個變量。目前成熟的技術(shù)主要用于低速緩慢的大型重載工程汽車和裝甲車上,研發(fā)的熱點和難點是將分布式輪轂驅(qū)動用于城市交通電動汽車上。文獻[5]將BP神經(jīng)網(wǎng)絡(luò)用于轉(zhuǎn)速分配及控制,可用于和學(xué)習(xí)樣本類似的車輛情況和路況。文獻[6]根據(jù)橫擺角速度、橫向加速度與參照速度的誤差值和后續(xù)的PI 控制環(huán)節(jié)進行轉(zhuǎn)矩分配。文獻[7]根據(jù)橫擺角速度、質(zhì)心側(cè)偏角與參考值間的差值,采用滑模控制來計算所需要的總橫擺力矩,優(yōu)化分配各個輪胎受力。目前的研究基本是在特定的車輛實例中針對某一個目標(biāo),例如滑移率[8]、側(cè)向力[8]、橫擺角速度等,進行轉(zhuǎn)矩分配或者轉(zhuǎn)速分配來提高車輛操縱性和穩(wěn)定性,控制效果滿意。但控制模型及控制參數(shù)的調(diào)整,動力學(xué)特性和動力學(xué)參數(shù),包括電機的參數(shù)和選擇千差萬別,沒有通用的參照可以使用,而且很多研究只考慮車輛的動力學(xué),忽略電機本身的動力學(xué)特性和車輛動力學(xué)特性的耦合,把驅(qū)動電機看作是一個理想的完美驅(qū)動單元[9]。本文在前期輪轂電機驅(qū)動研究的基礎(chǔ)上[10-12],首先分析整車動力學(xué)模型,在整車動力學(xué)模型上增加了直流電機驅(qū)動模型,把驅(qū)動電機機電特性和車輛動力學(xué)模型集成起來,針對后輪輪轂電機驅(qū)動的特定車輛,在特定行駛速度下仿真分析轉(zhuǎn)向情況下的穩(wěn)定性控制特性。
1 輪轂驅(qū)動電機及整車動力學(xué)模型
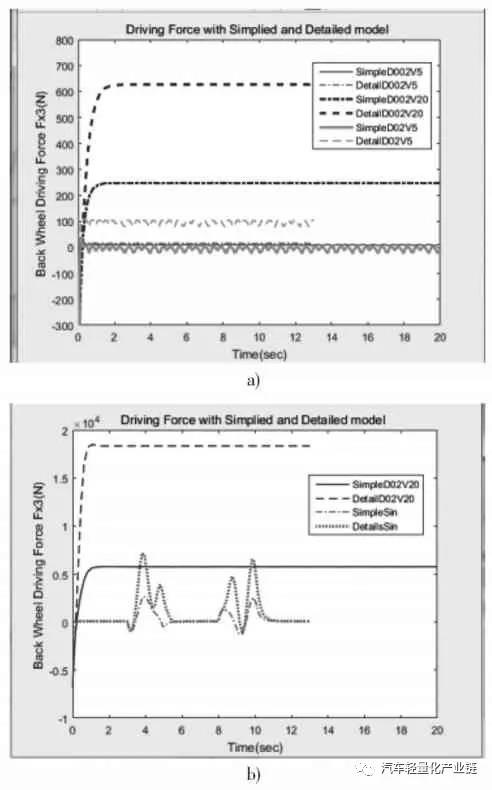
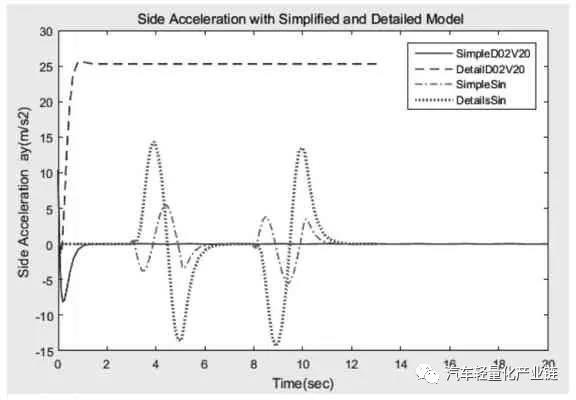
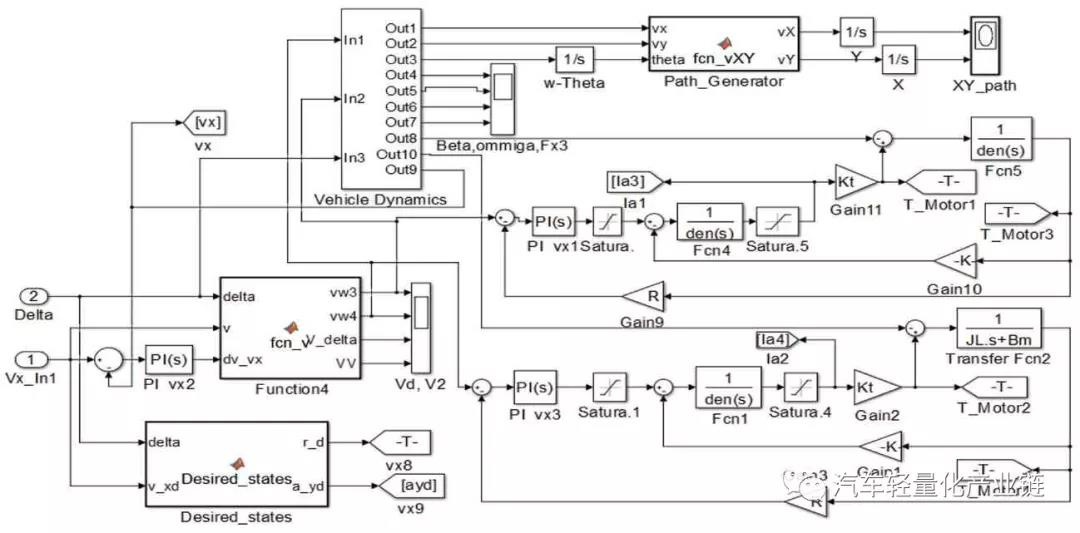
電動汽車的可靠行駛和操控要求輪轂電機具有寬的調(diào)速范圍、足夠大的啟動轉(zhuǎn)矩、體積小、重量輕,制動性能好,且具有能量回饋的特性。本文主要研究直流電機作為后輪驅(qū)動,直流電機產(chǎn)生的電磁轉(zhuǎn)矩帶動車輪旋轉(zhuǎn),同時克服由于摩擦產(chǎn)生的阻力和負(fù)載轉(zhuǎn)矩。對電機而言,車輪和地面的摩擦力形成的轉(zhuǎn)矩為負(fù)載轉(zhuǎn)矩,對車輛來說,這個與輪胎變形相關(guān)的摩擦力就是車輪前進的驅(qū)動力,機電耦合的電磁轉(zhuǎn)矩方程、直流電機的電樞回路電壓平衡方程(電方程)如式(1)~式(3)所示:式中:Te 為電磁轉(zhuǎn)矩,與電樞電流ia(t)成正比;J 為車輪與電機的轉(zhuǎn)動慣量;R 為車輪半徑;Ua( )t 為電樞電壓;w(t)為電機轉(zhuǎn)速;La,Ra 分別為電樞電路的電感和電阻;Fx 為車輪縱向摩擦力,當(dāng)車輪橫向力一定時,縱向力取決于車輪的滑轉(zhuǎn)率,在滑轉(zhuǎn)率很小時(對于干路面滑轉(zhuǎn)率小于 0.1),縱向力與滑轉(zhuǎn)率成正比[2];Bm,Ke,Kt 分別為粘性摩擦系數(shù)、電勢系數(shù)和轉(zhuǎn)矩系數(shù),由電機設(shè)計參數(shù)得出;i=1,2,3,4,表示汽車的4 個輪子,分別為左前輪、右前輪、左后輪和右后輪;νwi 為車輪轉(zhuǎn)速;νi 為車輪中心速度平行于車輪平面的分量;Cx 為車輪的縱向剛度。本文研究的是后輪輪轂電機驅(qū)動的電動汽車,2 個后輪輪轂上分別安裝2 個直流驅(qū)動電機,在驅(qū)動轉(zhuǎn)矩作用下,2 個后輪輪胎受到地面的縱向摩擦力。轉(zhuǎn)向時,根據(jù)轉(zhuǎn)角及當(dāng)前的速度,在后輪上分配不同的速度和力矩,形成側(cè)向摩擦力,側(cè)向摩擦力和縱向摩擦力的合成轉(zhuǎn)矩完成汽車的轉(zhuǎn)彎。設(shè)x 軸為汽車的前進方向(縱向),y 為與車身垂直的水平(橫向)方向,汽車行駛或者轉(zhuǎn)彎時,車輛中心具有縱向平動(縱向速度為Vx)、橫向平動(橫向速度為Vy)和在地平面中繞z 軸的轉(zhuǎn)動(橫擺角速度為ω)三個自由度方向的運動,考慮車身受到的空氣阻力,可得到以下縱向運動、橫向運動和橫擺轉(zhuǎn)動的動力學(xué)方程組[13]:式中:δ 為前輪轉(zhuǎn)向角;A 為車輛質(zhì)心到前軸的距離;B 為車輛質(zhì)心到后軸的距離;W 為左右輪距;M 為車輛質(zhì)量;J 為車輛轉(zhuǎn)動慣量。在縱向運動方向上考慮空氣的阻力,與空氣阻力相關(guān)的參數(shù)分別為空氣阻力系數(shù)CD,車輛正面迎風(fēng)面積A,空氣密度ρ。每個車輪的中心沿著車輪縱向的速度由式(7)計算,由于車輪的側(cè)向彈性形變,車輪中心速度與車輪平面成一夾角,形成車輪的側(cè)偏角αi,具體計算如下:當(dāng)車輪側(cè)偏角較小時輪胎側(cè)偏特性處于線性區(qū),車輪受到的垂直方向的力一定時,側(cè)向力Fyi 與側(cè)偏角成正比[14],比例系數(shù)Cy 為車輪的側(cè)偏剛度,本文取輪胎摩擦公式的線性段的斜率值。一般文獻進行計算分析時,為了降低計算難度,通常忽略橫向加速度和縱向加速度的耦合作用。從公式本身來看,如果轉(zhuǎn)角和線速度都比較小時,簡化模型可以近似反映運動情況,引起的誤差比較小,但是當(dāng)轉(zhuǎn)角或者速度較大時,簡化模型就會產(chǎn)生較大的誤差。如果忽略這種耦合,對直線行駛沒有什么影響,但在有轉(zhuǎn)彎的狀況下,轉(zhuǎn)角越大速度越大,誤差越大。分別對轉(zhuǎn)角為0.2 rad 和0.02 rad,車輛質(zhì)心線速度為5 m/s 和20 m/s形成的四種行駛狀況,以及雙移線行駛狀況共五種狀態(tài)定量分析簡化模型和非簡化模型的動力學(xué)特性,求解結(jié)果前三種工況組合下左后輪的縱向驅(qū)動力Fx3,如圖1所示。由圖1 可以看出,當(dāng)轉(zhuǎn)角很小δ=0.02 rad,行駛速度很小v=5 m/s 時,兩種模型的縱向驅(qū)動力差別很小,簡化模型作為力學(xué)模型引起的誤差很小,可以忽略。當(dāng)速度增加到20 m/s 時,簡化模型的縱向驅(qū)動力為200 N 以上(SimpleD002V20),而非簡化模型的縱向力需要600 N以上(DetailD002V20),增加了2 倍,轉(zhuǎn)向和縱向運動的耦合不容忽視。繼續(xù)觀察δ=0.2 rad 時,v=5 m/s 和v=20 m /s 時 的 曲 線(SimpleD02V20 和 DetailD02V20,SimpleD02V5 和 DetailD02V5),可以看出隨著轉(zhuǎn)角 δ 和速度v 的增加,簡化模型和詳細模型中縱向驅(qū)動力的差別也會增大;圖1b)的雙移線運動狀況是速度不變、轉(zhuǎn)角進行兩個周期的正弦變化時的縱向驅(qū)動力結(jié)果,可以看出,縱向驅(qū)動力的差別也是隨著轉(zhuǎn)角的增大而增大。模型的橫向驅(qū)動力和側(cè)偏角也是隨著轉(zhuǎn)角和速度的增大而增大。圖2 為側(cè)向加速度的比較,可以看出,行駛速度較大時,兩種模型的橫向加速度是有一定的相位差的,即在正弦變化的轉(zhuǎn)角輸入中,兩種模型達到最大橫向加速度的時間不同。由此可見,在轉(zhuǎn)角較大、速度較大時,簡化模型已經(jīng)不能準(zhǔn)確及時地反映行駛的動力學(xué)特性,因此本研究在后續(xù)的控制模型中采用反映橫向運動和橫擺角速度耦合的詳細模型。整體動力學(xué)及控制模型如圖3 所示,圖中整車動力學(xué)模型封裝為子模型。圖3 整車動力學(xué)及后輪驅(qū)動電機兩層三環(huán)節(jié)控制模型
在詳細動力學(xué)模型中,給總體行駛速度加上速度反饋及PI 控制,形成第一層外環(huán)的速度控制,再把兩個驅(qū)動電機及其控制模型集成到整個模型的車輪部分中,把后輪3 和后輪4 的車輪速度和車輪負(fù)載分別作為兩個驅(qū)動電機模型的輸入,根據(jù)設(shè)定的速度和轉(zhuǎn)角,采用Ackermann 模型進行兩個后輪的速度分配,形成兩個驅(qū)動電機的速度參考,每個電機的輪速反饋和PI 控制形成第二層內(nèi)環(huán)的兩個控制環(huán)節(jié),形成后輪輪轂驅(qū)動的整體電動汽車控制模型。車輛的主要參數(shù)及根據(jù)車輛要求設(shè)計的直流電機主要參數(shù)為:M=1 500;A=1.6;B=1.4;W=1.6;J=3 375;R=0.3;Ke=4.5;Kt=43;La=0.012;Ra=1.2;Bm=0.005,控制參數(shù)根據(jù)模型進行整定和優(yōu)化。仿真分析中對三種控制模型進行對比:第一種是沒有速度反饋的原始模型;第二種是只加一層速度反饋而沒有集成兩個驅(qū)動電機模型,把驅(qū)動電機作為一個理想的驅(qū)動單元;第三種則是本文具有兩層反饋三個控制環(huán)節(jié)的模型(見圖3)。在后續(xù)的仿真分析對比中,第二種只有一層PID 控制的數(shù)據(jù)標(biāo)記為with PID,第三種集成車輛模型和電機模型的數(shù)據(jù)標(biāo)記為with PID and Motor,剩下的數(shù)據(jù)為沒有速度反饋環(huán)節(jié)的第一種原始模型。仿真分析中的汽車穩(wěn)定性系數(shù)Kus 由回歸得出,側(cè)向剛度和縱向剛度取輪胎魔術(shù)公式中的斜率部分,路況為干性平坦路面。本文主要分析轉(zhuǎn)彎時的控制,工況為行駛速度恒定下的兩次變道雙移線,速度設(shè)為v=20 m/s=72 km/h。轉(zhuǎn)角變化分析兩種情況:第一種是轉(zhuǎn)角突然階躍變化左-右-直-右-左,實現(xiàn)兩次變道;第二種是把階躍變換調(diào)整為相同頻率的正弦變化,峰值為7°,頻率為0.5,兩個正弦波之間隔1.5 個周期,即直行1.5 個周期,兩種輸入狀態(tài)下的轉(zhuǎn)角如圖4 所示。圖5 和圖6 分別顯示兩種輸入模式下三種模型的后輪驅(qū)動力和橫向加速度曲線對比。可以看出,對于表示突然轉(zhuǎn)向的階躍輸入,會引起加速度響應(yīng)的突然變化,驅(qū)動力變化曲線不平穩(wěn),有突然變化的尖角,導(dǎo)致側(cè)向不穩(wěn)定;調(diào)整成為正弦變化雙移線后消除了曲線尖角,驅(qū)動力曲線平緩很多,幅值也有較大程度的下降,車輛的穩(wěn)定程度有明顯的提高,這和一般的駕駛體驗相符,說明控制模型能正確模擬實際的狀況。第三種模型和第一種模型的側(cè)向加速度幅值比第二種模型小點,但是第一種模型因為沒有反饋環(huán)節(jié),因而無法跟蹤參照速度,導(dǎo)致縱向速度略微降低,穩(wěn)態(tài)誤差加大,即犧牲一部分縱向速度,達到減少側(cè)向加速度的目的。綜合比較,第三種模型縱向速度始終跟隨參照速度,同時側(cè)向加速度也比其他模型小,因此轉(zhuǎn)向穩(wěn)定性較好。
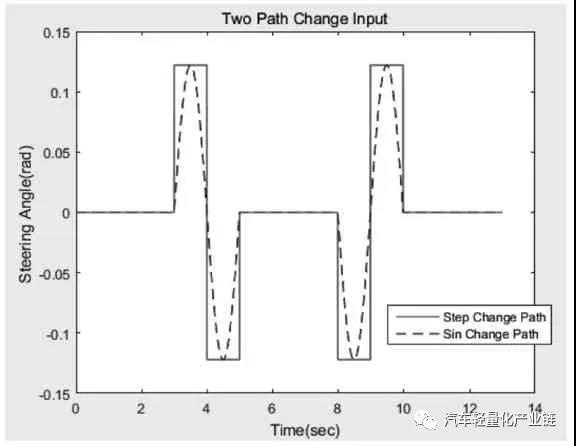
圖4 轉(zhuǎn)角輸入階躍變化和調(diào)整后的正弦變化
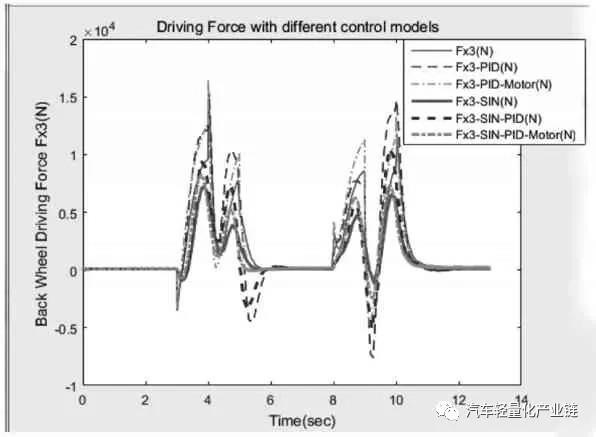
圖5 轉(zhuǎn)角階躍和正弦響應(yīng)的后輪驅(qū)動力
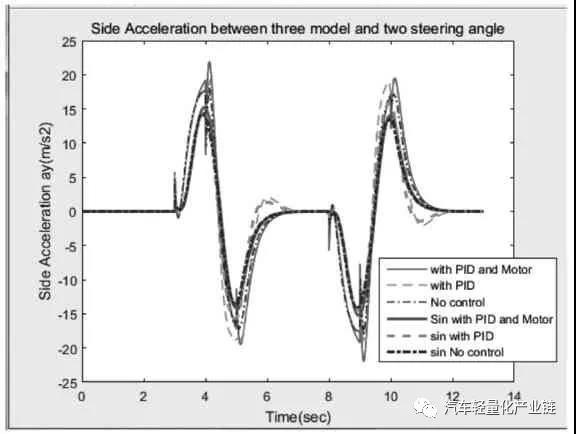
圖6 轉(zhuǎn)角階躍和正弦響應(yīng)的側(cè)向加速度
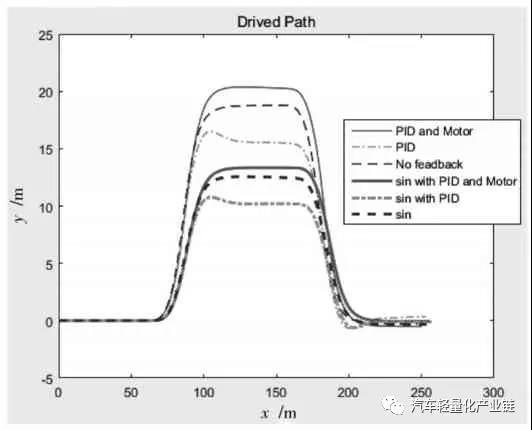
圖7 顯示了三種模型兩種輸入的雙移線軌跡。首先比較正弦調(diào)整的轉(zhuǎn)角輸入和階躍變化工況,由于正弦轉(zhuǎn)角變化相對減緩且數(shù)值偏小,導(dǎo)致橫向加速度變小進而橫向速度變小,因而y 方向的位移相應(yīng)減少;對于有PID 和電機模型的兩層三控制環(huán)節(jié)模型,由于行駛速度和單個輪速的及時反饋和補償,縱向速度和橫向速度都能跟蹤參照速度,不足轉(zhuǎn)向和過度轉(zhuǎn)向能夠得到及時控制,因而y 方向的位移是三個模型中最大的,也就是說,達到相同的y 方向位移的參照速度可以降低;對于只有外層控制環(huán)節(jié)的第二種模型,由于不能及時調(diào)整兩個輪子的速度,同樣輸入情況下會出現(xiàn)過度轉(zhuǎn)向或轉(zhuǎn)向不足的情況。圖7 轉(zhuǎn)角階躍和正弦響應(yīng)的行駛軌跡
本文建立并集成了驅(qū)動電機模型和整車動力學(xué)模型,形成后輪驅(qū)動整車控制模型。考慮通常的忽略橫向加速度和縱向加速度的耦合作用,量化分析簡化模型和非簡化模型在不同轉(zhuǎn)角和速度時的輸入輸出特性,認(rèn)為在轉(zhuǎn)角和速度較大時,簡化模型不能準(zhǔn)確及時地進行動力學(xué)控制,因此本文采用反映橫向運動和縱向運動耦合的詳細模型。在控制框架中,輪速和與輪速相關(guān)的負(fù)載轉(zhuǎn)矩作為機電模型的輸入,外層進行總行駛速度反饋控制,內(nèi)層進行兩個電機轉(zhuǎn)速的反饋控制,形成一個兩層三環(huán)節(jié)的控制模型,外層的總行駛速度經(jīng)過內(nèi)外輪的速度分配即電子差速,作為內(nèi)層兩個電機轉(zhuǎn)速的輸入分別控制兩個驅(qū)動電機。最后對三種模型在兩種轉(zhuǎn)角變化工況下的動力學(xué)響應(yīng)進行對比分析,驗證了該控制方法可以達到預(yù)期的效果。
[1]李以農(nóng),楊陽.電動汽車底盤一體化控制技術(shù)的發(fā)展趨勢與展望[J].世界科技研究與發(fā)展,2016,38(3):481-491.[2]楊世春.電動汽車設(shè)計基礎(chǔ)[M].北京:國防工業(yè)出版社,2013:24-25.[3]徐寅,陳東.電動汽車差速系統(tǒng)研究綜述[J].中國機械工程,2011,22(4):498-503.[4]袁儀,陳世元,劉耀閣.電動汽車電子轉(zhuǎn)彎差速的解決方案綜述[J].上海汽車,2009(3):2-5.[5]唐文武,陳世元,郭建龍.基于BP神經(jīng)網(wǎng)絡(luò)的電動車電子差速器設(shè)計[J].汽車工程,2007,29(5):437-440.[6]OSBORNA R,SHIMB T.Independent control of all-wheeldrive torque distribution [J].Vehicle system dynamics,2006,44(7):529-546.[7]余卓平,姜煒,張立軍.四輪輪轂電機驅(qū)動電動汽車扭矩分配控制[J].同濟大學(xué)學(xué)報,2008,36(8):1115-1119.[8]葛英輝,倪光正.新的輪式驅(qū)動電動車電子差速控制算法的研究[J].汽車工程,2005,27(3):340-343.[9]KAROGAL I,AYALEW B.Independent torque distribution strategies for vehicle stability control [R].Detroit:Sae World Congress & Exhibition,2009.[10]史秀梅,鄭壽森,祁新梅,等.三相開關(guān)磁阻電動機電磁場有限元分析[J].微特電機,2009(12):35-37.[11]熊俊峰,鄭壽森,祁新梅,等.電動汽車開關(guān)磁阻電機驅(qū)動電源的設(shè)計與研究[J].電力電子技術(shù),2009(7):42-44.[12]史秀梅,鄭壽森,祁新梅,等.電動汽車用開關(guān)磁阻電機有限元分析及仿真[J].系統(tǒng)仿真學(xué)報,2011,23(7):1374-1377.[13]王強,王耘,宋小文.基于差動驅(qū)動的電子差速控制方法研究[J].機電工程,2011,28(6):698-703.[14]韋競秋.汽車工程應(yīng)用力學(xué)[M].北京:機械工業(yè)出版社,2013:17-18.[15]余卓平,趙治國,陳慧.主動前輪轉(zhuǎn)向?qū)囕v操縱穩(wěn)定性能的影響[J].中國機械工程,2005,16(7):652-657.